AkashJain

We all carry an intuitive sense of chaos. The Cambridge Dictionary describes chaos as “a state of total confusion with no order.” In scientific contexts, chaos refers to the loss of predictability in a physical system or mathematical model arising from the sheer scale and complexity of its components. More precisely, chaos is a nonequilibrium phenomenon in which the time evolution of a system is extraordinarily sensitive to its initial conditions. Minuscule, often imperceptible, changes in those initial conditions can dramatically alter the system’s long-term trajectory, a feature commonly known as the butterfly effect.

The above definition of chaos works well for classical deterministic systems. By contrast, evolution in quantum systems does not follow definite trajectories, which makes it harder to pin down what it means for a quantum system to exhibit chaos. A particularly promising way to quantify quantum chaos involves the so-called Out-of-Time-Ordered Correlators (OTOCs); see García-Mata et al. for more details. For readers familiar with quantum mechanics, OTOCs compute the expectation value of the square of the commutator between an observable and its initial value. In quantum-chaotic systems, OTOCs typically begin near zero, then exhibit a period of rapid exponential growth characteristic of chaotic behavior, and finally fluctuates around a saturation value at late times when the system has effectively lost all memory of its initial state. For non-chaotic systems, the intermediate growth behaviour is absent.

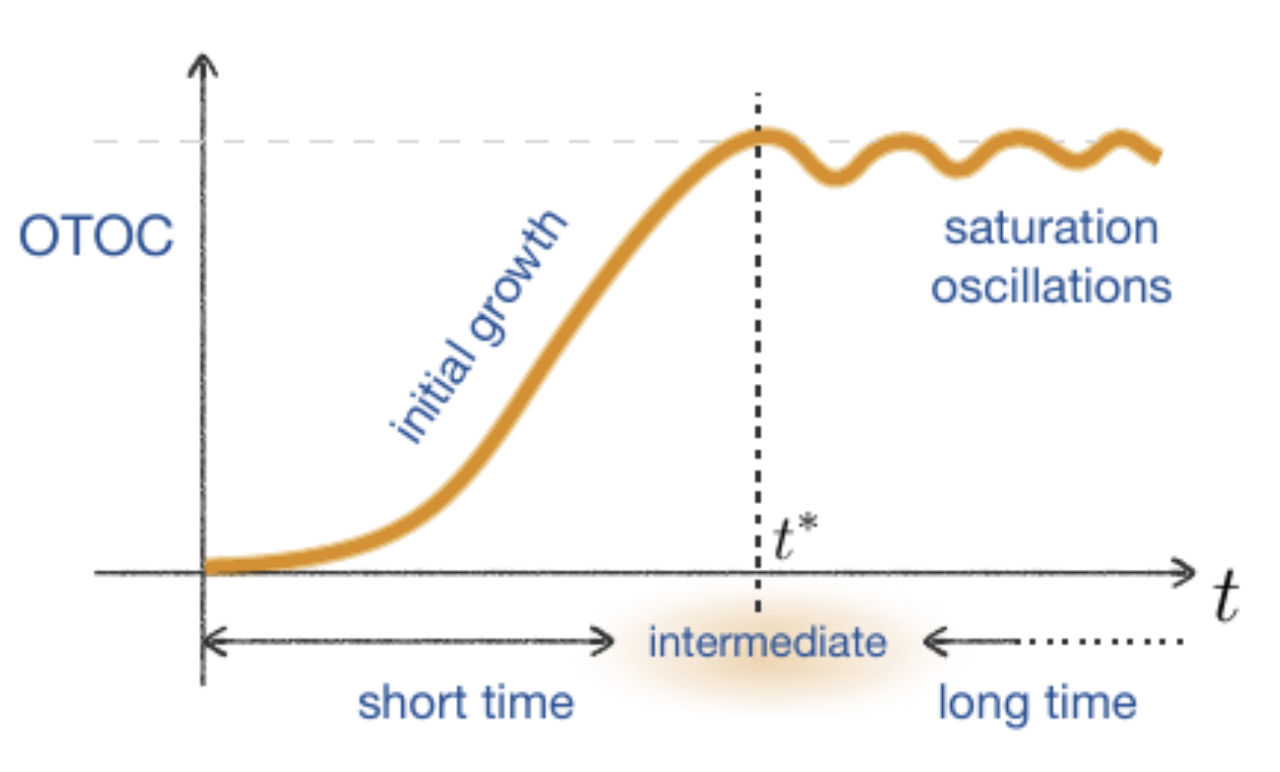
My research programme at Oxford with Prof. Mark Mezei focuses on constructing low-energy effective field theory (EFT) models for chaotic quantum systems. These models allow us to compute OTOCs and explore how they interact with other non-equilibrium phenomena such as dissipation. We are applying modern Schwinger-Keldysh EFT techniques, a framework that evolves multiple copies of a physical system forward and backward in time, as well as insights from holographic dualities. I will share updates as the results develop.

Collaborators